University of Alberta Dictionary of Cognitive Science: Standard Pattern Associator

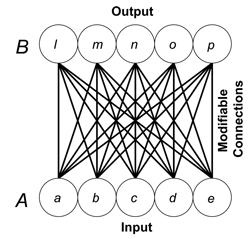
The standard pattern associator is a basic distributed memory consisting of fully connected sets of input and output units. Usually the memory begins as a blank slate: all of the connections between processors start with weights equal to zero. During a learning phase, pairs of to-be-associated patterns simultaneously activate the input and output units. With each presented pair, all of the connection weights – the strength of each connection between an input and an output processor -- are modified by adding a value to them. This value is determined in accordance with some version of Hebb’s (1949) learning rule. Usually, the value added to a weight is equal to the activity of the processor at the input end of the connection, multiplied by the activity of the processor at the output end of the connection, multiplied by some fractional value called a learning rate. The mathematical details of such learning are provided in Chapter 9 of Dawson (2004).

The standard pattern associator is called a distributed memory because its knowledge is stored throughout all the connections in the network, and because this one set of connections can store several different associations. During a recall phase, a cue pattern is used to activate the input units. This causes signals to be sent through the connections in the network. These signals are equal to the activation value of an input unit multiplied by the weight of the connection through which the activity is being transmitted. These signal, are used by the output processors to compute their net input, which is simply the sum of all of the incoming signals. In the standard pattern associator, an output unit’s activity is equal to its net input. If the memory is functioning properly, then the pattern of activation in the output units will be the pattern that was originally associated with the cue pattern.

The standard pattern associator is the cornerstone of many models of memory created after the cognitive revolution (Anderson, 1972; Anderson, Silverstein, Ritz, & Jones, 1977; Eich, 1982; Hinton & Anderson, 1981; Murdock, 1982; Pike, 1984; Steinbuch, 1961; Taylor, 1956). These models are important, because they use a simple principle – James’ (1890) law of habit -- to model many subtle regularities of human memory, including errors in recall.

References:

Anderson, J. A. (1972). A simple neural network generating an interactive memory. Mathematical Biosciences, 14, 197-220.
Anderson, J. A., Silverstein, J. W., Ritz, S. A., & Jones, R. S. (1977). Distinctive features, categorical perception and probability learning: Some applications of a neural model. Psychological review, 84, 413-451.
Dawson, M. R. W. (2004). Minds And Machines : Connectionism And Psychological Modeling. Malden, MA: Blackwell Pub.
Eich, J. M. (1982). A composite holographic associative recall model. Psychological Review, 89, 627-661.
Hebb, D. O. (1949). The Organization Of Behaviour. New York: John Wiley and Sons.
Hinton, G. E., & Anderson, J. A. (1981). Parallel Models Of Associative Memory. Hillsdale, NJ: Lawrence Erlbaum Associates.
Murdock, B. B. (1982). A theory for the storage and retrieval of item and associative information. Psychological Review, 89, 609-626.
Pike, R. (1984). Comparison of convolution and matrix distributed memory systems for associative recall and recognition. Psychological Review, 91, 281-294.
Steinbuch, K. (1961). Die lernmatrix. Kybernetik, 1, 36-45.
Taylor, W. K. (1956). Electrical simulation of some nervous system functional activities. In C. Cherry (Ed.), Information Theory (pp. 314-328). London: Butterworths Scientific Publications

(Added October 2010)